Бинарна претрага елемента у низу
Алгоритам бинарне претраге вредности у низу одговара оном који се може применити у игри погађања непознатог броја и који је заснован на половљењу интервала. Основна идеја је да се тражени елемент пореди са средишњим елементом у низу. Ако је тражени елемент мањи од средишњег, пошто је низ сортиран, знаћемо да је мањи и од свих елемената десно од тог средишњег, па тај део низа можемо елиминисати (можемо начинити одсецање у претрази) и претрагу можемо наставити само у левој половини низа. Симетрично, ако је тражени елемент већи од средишњег, због сортираности је већи и од свих елемената лево од средишњег и лева половина низа може бити елиминисана из даље претраге. На крају, ако елемент није ни мањи ни већи од средишњег, онда му је једнак и пронађен је у низу. Приметимо да у основи алгоритма бинарне претраге лежи техника одсецања, која је оправдана тиме што је низ сортиран.
Пошто се у сваком кораку претраге дужина низа дупло смањује, за претрагу целог низа довољно је \(O(\log{n})\) корака, где је \(n\) дужина низа. Наиме, претрага у најгорем случају траје све док се половљењем низ не испразни. Дужина низа након \(k\) корака половљења је отприлике \(\frac{n}{2^k}\). Низ ће се испразнити када је \(\frac{n}{2^k} < 1\), тј. када је \(n < 2^k\), тј. када је \(k > \log_2{n}\).
Слично као и за сортирање, већина програмских језика пружа готове библиотечке функције за бинарну претрагу.
У језику C++ функција binary_search проверава да ли дати
распон елемената (задат помоћу два итератора) садржи задату вредност
(функција враћа true ако и само ако се тражени елемент
налази унутар задатог распона). Тако се провера да ли се дати елемент
x налази унутар сортираног вектора a може
извршити помоћу binary_search(begin(a), end(a), x).
Поред ове, постоје још три функције које врше одређене варијације
бинарне претраге. Ако је потребно пронаћи све елементе једнаке датом,
можемо користити функцију equal_range (са истим параметрима
као binary_search). Она враћа пар итератора који
ограничавају распон елемената једнаких датом (први итератор указује на
први елемент једнак траженој вредности, а други на позицију непосредно
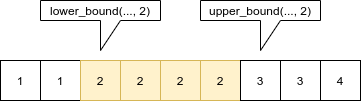
иза последњег елемента једнаког траженој вредности). Функција
lower_bound враћа први од та два итератора (тј. први
елемент који је већи или једнак од тражене вредности), а функција
upper_bound враћа други од њих (тј. први елемент који је
строго већи од тражене вредности).
О њима и њиховој употреби ће бити више речи у наредним поглављима.
У свим библиотечким функцијама за бинарну претрагу, ако се не зада другачије, подразумева се да је низ сортиран у односу на подразумевани поредак елемената (неопадајући нумерички ако су бројеви у питању, тј. неопадајући абецедни лексикографски ако су ниске у питању). Поредак се може задати или променити на сличан начин као код функција за сортирање (о чему ће бити више речи касније).
Бинарна претрага елемента у низу
Алгоритам бинарне претраге вредности у низу одговара оном који се може применити у игри погађања непознатог броја и који је заснован на половљењу интервала. Основна идеја је да се тражени елемент пореди са средишњим елементом у низу. Ако је тражени елемент мањи од средишњег, пошто је низ сортиран, знаћемо да је мањи и од свих елемената десно од тог средишњег, па тај део низа можемо елиминисати (можемо начинити одсецање у претрази) и претрагу можемо наставити само у левој половини низа. Симетрично, ако је тражени елемент већи од средишњег, због сортираности је већи и од свих елемената лево од средишњег и лева половина низа може бити елиминисана из даље претраге. На крају, ако елемент није ни мањи ни већи од средишњег, онда му је једнак и пронађен је у низу. Приметимо да у основи алгоритма бинарне претраге лежи техника одсецања, која је оправдана тиме што је низ сортиран.
Пошто се у сваком кораку претраге дужина низа дупло смањује, за претрагу целог низа довољно је \(O(\log{n})\) корака, где је \(n\) дужина низа. Наиме, претрага у најгорем случају траје све док се половљењем низ не испразни. Дужина низа након \(k\) корака половљења је отприлике \(\frac{n}{2^k}\). Низ ће се испразнити када је \(\frac{n}{2^k} < 1\), тј. када је \(n < 2^k\), тј. када је \(k > \log_2{n}\).
Слично као и за сортирање, већина програмских језика пружа готове библиотечке функције за бинарну претрагу.
У језику C# функција Array.BinarySearch врши бинарну
претрагу сортираног низа. Функцији се задаје обавезно низ и вредност
која се тражи. Функција враћа било коју позицију на којој је тражена
вредност пронађена или негативан број који је битовска негација позиције
првог елемента строго већег од тражене вредности (тј. дужине низа ако
такав елемент не постоји). Зато проверу да ли низ a садржи
елемент x можемо извршити помоћу услова
Array.BinarySearch(a, x) >= 0. Ако је потребно
претражити само део низа, тада је могуће као додатне параметре
проследити индекс почетка и број елемената дела низа који се
претражује.
Ако се претражује сортирана листа, користи се метода
BinarySearch, која се понаша скоро потпуно исто као
Array.BinarySearch (једино што се листа не наводи као
аргумент, већ се метода позива на листи). На пример, провера да ли
сортирана листа a садржи елемент x може се
извршити позивом a.BinarySearch(x) >= 0.
У свим библиотечким функцијама за бинарну претрагу, ако се не зада другачије, подразумева се да је низ сортиран у односу на подразумевани поредак елемената (неопадајући нумерички ако су бројеви у питању, тј. неопадајући абецедни лексикографски ако су ниске у питању). Поредак се може задати или променити на сличан начин као код функција за сортирање (о чему ће бити више речи касније).
